b. 気温はどこまで上昇？

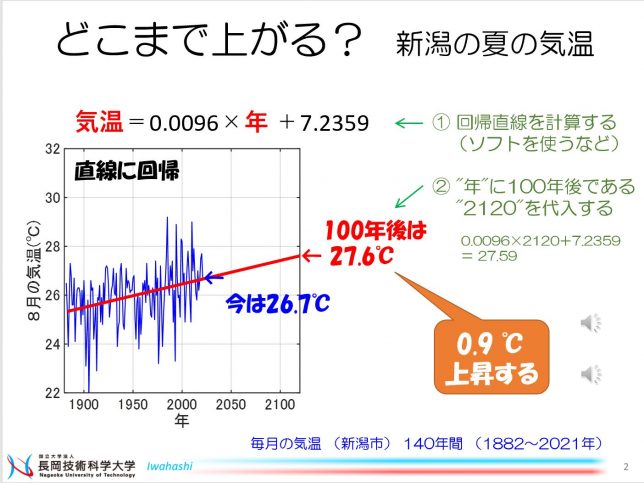
今、手元には新潟市の8月の気温データがあります。このデータの値を青い線でプロットしました。これらを近似する直線を赤い線で示します。この直線を100年後まで延長すると、気温が 27.6度になりました。今よりも 0.9度、上昇することになります。

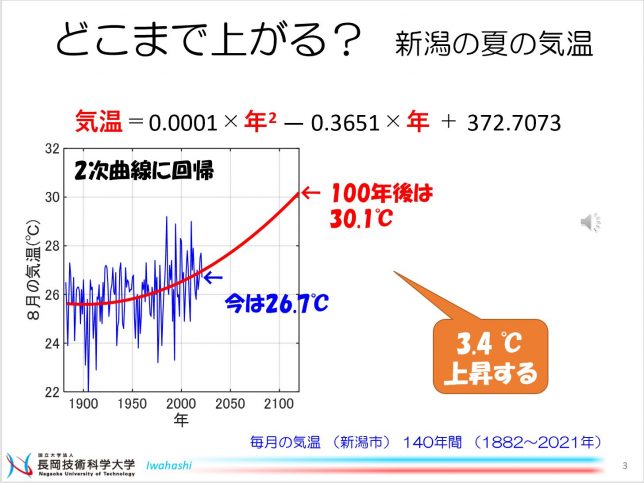
このような近似直線は「線形回帰」を使うことで得られます。「最小二乗法」という最適化のしくみにより、直線の傾きと切片が、観測データから一意に定まります。直線ではなく「曲線」も得られます。右図は2次曲線の例です。100年後には今よりも 3.4度、上昇することになりました。

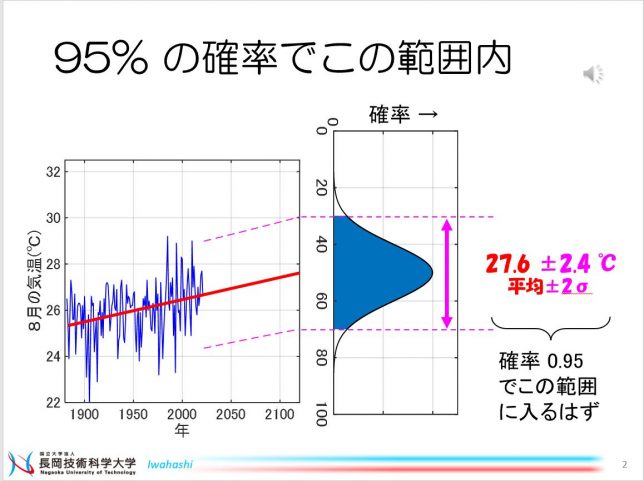
これまでに、線形回帰を使って先々の値を予測する方法をみてきました。予測結果は「値」として得られました。これを点推定といいます。次は、区間推定の話です。予測結果を、ある値として点で示すのではなく、ここからここまでの範囲、というように「区間」で示します。値としてぴたりと当てるのではなく、区間として確率的に予測します。

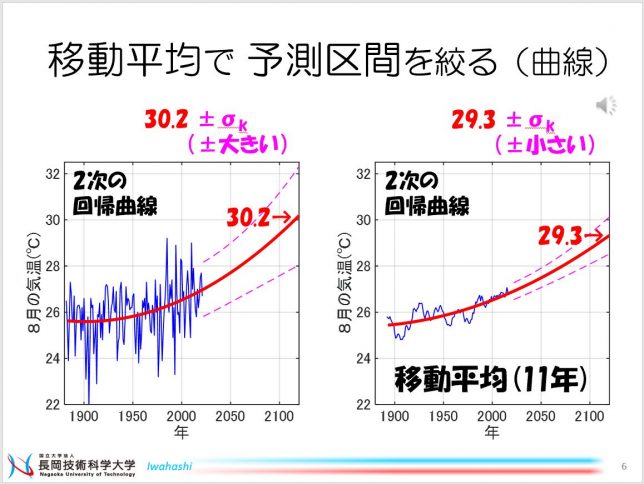
観測データに、移動平均を適用すると、どうなるでしょうか？ 右側のグラフでは、11年間の移動平均を使いました。青で示されるように、気温の細かい上下の変動、つまり、縦軸方向のバラツキが抑えられて、滑らかな変化となりました。この平滑化されたデータに対して、区間推定を適用した結果、 区間の幅は ±0.4 度となりました。

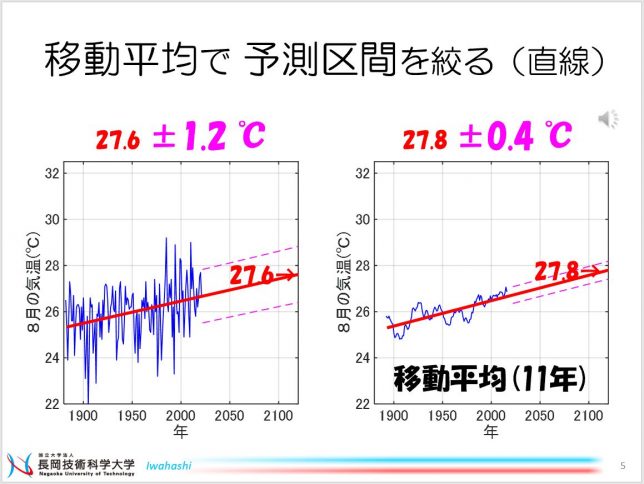
予測値がバラつく幅は、何によって決まるでしょうか？　回帰直線からみて、観測データがバラついていると、予測結果もやはりバラつきます。予測に使ったデータ数が少ないと、バラつきの幅は広がります。データ数が少ないときも、あまり良い結果は期待できません。出来るだけ近い未来について、過去のデータが沢山あって、その殆どが回帰直線上にぴったりと乗っていれば、区間の幅は狭くなるので、予測は当たります。